الگوریتم DBSCAN

خوشه‌بندی یکی از روش‌های یادگیری بدون نظارت است که داده‌ها را به چندین گروه یا خوشه خاص تقسیم می‌کند. در این روش، داده‌هایی که ویژگی‌های مشابهی دارند در یک گروه قرار می‌گیرند، و داده‌هایی که از نظر ویژگی متفاوت هستند به گروه‌های جداگانه‌ای تقسیم می‌شوند.

این روش شامل متدهای مختلفی است که بر اساس معیارهای فاصله متفاوت عمل می‌کنند. برای مثال:

• K-Means (فاصله بین نقاط)
• Affinity Propagation (فاصله گراف)
• Mean-Shift (فاصله بین نقاط)
• DBSCAN (فاصله بین نزدیک‌ترین نقاط)
• Gaussian Mixtures (فاصله Mahalanobis تا مراکز)
• Spectral Clustering (فاصله گراف)

مرکزی‌ترین رویکرد در همه این متدها محاسبه شباهت‌ها و سپس خوشه‌بندی داده‌ها بر اساس آن است. درادامه بیشتر با روش خوشه‌بندی مبتنی بر چگالی یا DBSCAN آشنا خواهیم شد.

الگوریتم DBSCAN یا خوشه‌بندی مبتنی بر چگالی چیست؟

خوشه‌بندی مبتنی بر چگالی روشی در یادگیری بدون نظارت است که خوشه‌ها را بر اساس نواحی پیوسته با چگالی بالا شناسایی می‌کند. این نواحی با نواحی با چگالی پایین از هم جدا می‌شوند.

DBSCAN، که مخفف “Density-Based Spatial Clustering of Applications with Noise” است، یک الگوریتم پایه برای این نوع خوشه‌بندی است. این الگوریتم می‌تواند خوشه‌هایی با اشکال و اندازه‌های مختلف را در داده‌هایی که دارای نویز و نقاط پرت هستند شناسایی کند.

چرا به الگوریتم DBSCAN نیاز داریم؟

یکی از چالش‌های الگوریتم K-Means این است که ممکن است داده‌هایی که رابطه ضعیفی دارند را در یک خوشه قرار دهد. در K-Means، هر داده‌ای به یک خوشه اختصاص می‌یابد، حتی اگر از نظر فاصله بسیار دور باشد. همچنین، تغییرات کوچک در داده‌ها می‌توانند نتیجه خوشه‌بندی را تغییر دهند.

از طرفی، در K-Means باید تعداد خوشه‌ها (k) از پیش مشخص باشد، که در بسیاری از مواقع مقدار مناسبی برای آن در دسترس نیست.

DBSCAN این مشکلات را حل می‌کند. در DBSCAN نیازی به تعیین تعداد خوشه‌ها نیست. تنها نیاز است که یک تابع فاصله و معیاری برای تعیین فاصله “نزدیک” تعریف شود. این الگوریتم نتایج معقول‌تری نسبت به K-Means برای توزیع‌های مختلف ارائه می‌دهد.

پارامترهای DBSCAN

1. minPts:
   این پارامتر حداقل تعداد نقاط لازم در یک ناحیه را مشخص می‌کند تا ناحیه به عنوان خوشه در نظر گرفته شود. مقدار مناسب minPts به ابعاد داده‌ها و نویز موجود در مجموعه داده بستگی دارد و معمولاً باید بیشتر از ۳ انتخاب شود.
2. eps (ε):
   این پارامتر فاصله‌ای را تعیین می‌کند که در آن نقاط به عنوان همسایه در نظر گرفته می‌شوند. مقدار مناسب ε باید به دقت انتخاب شود؛ اگر بیش از حد کوچک باشد، خوشه‌های پراکنده ایجاد می‌شود و اگر بیش از حد بزرگ باشد، خوشه‌ها با هم ترکیب می‌شوند.
3. دسترسی چگالی:
   این مفهوم مشخص می‌کند که یک نقطه در صورتی به نقطه دیگری قابل دسترسی است که در فاصله ε از آن قرار داشته باشد. این ویژگی به شناسایی نواحی چگال و تشکیل خوشه‌ها کمک می‌کند.
4. اتصال چگالی:
   در این مفهوم، نقاط با استفاده از یک زنجیره متصل تعریف می‌شوند، به این صورت که هر نقطه در فاصله ε از نقطه قبلی باشد. این قابلیت امکان اتصال خوشه‌ها به صورت پویا و بدون تعیین تعداد خوشه‌ها را فراهم می‌کند.

انواع نقاط در DBSCAN

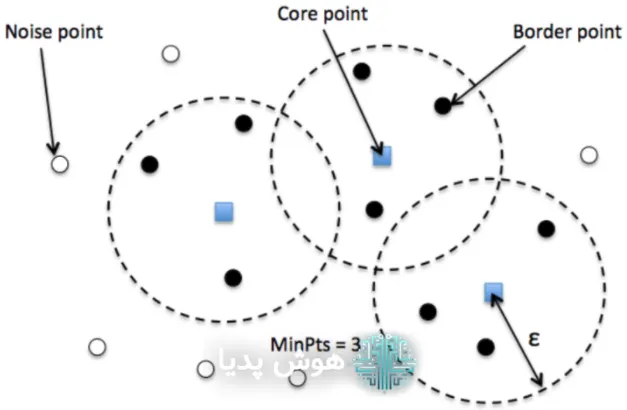
1. نقاط هسته‌ای (Core): نقاطی که تعداد کافی از همسایگان (حداقل minPts) در فاصله ε از آن‌ها وجود دارد.
2. نقاط مرزی (Border): نقاطی که در همسایگی یک نقطه هسته‌ای هستند، اما خودشان به اندازه کافی همسایه ندارند.
3. نویز (Noise): نقاطی که نه هسته‌ای هستند و نه در همسایگی نقاط هسته‌ای قرار دارند.

مراحل الگوریتم DBSCAN

مراحل اجرای الگوریتم به شرح زیر است:

1. به صورت تصادفی یک نقطه از مجموعه داده انتخاب می‌شود.
2. اگر تعداد نقاطی که در شعاع ε از این نقطه قرار دارند برابر یا بیشتر از minPts باشد، این نقاط به یک خوشه تعلق می‌گیرند.
3. این خوشه با محاسبه مکرر همسایگی هر نقطه گسترش می‌یابد.
4. این فرآیند برای تمام نقاط ادامه می‌یابد تا همه نقاط بررسی شوند.

تنظیم پارامترهای DBSCAN

1. minPts:
   • به صورت کلی، مقدار minPts باید حداقل ۳ باشد. برای داده‌های پرنویز یا بزرگ، مقادیر بالاتر پیشنهاد می‌شود.
   • یک قانون سرانگشتی: minPts = 2 × تعداد ابعاد داده.
2. ε:
   • انتخاب ε با استفاده از گراف فاصله k انجام می‌شود.
   • مقدار مناسب ε در جایی است که نمودار تغییر ناگهانی یا “آرنج” را نشان دهد.
3. تابع فاصله:
   • انتخاب تابع فاصله تأثیر مستقیم بر نتیجه الگوریتم دارد. این تابع باید متناسب با مجموعه داده انتخاب شود.

پیاده‌سازی کد الگوریتم DBSCAN با پایتون:

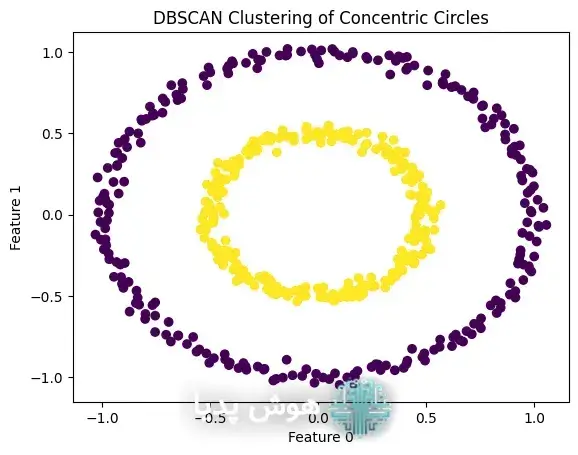
import matplotlib.pyplot as plt
from sklearn.datasets import make_circles
from sklearn.cluster import DBSCAN
import numpy as np

# ایجاد یک مجموعه داده با دایره‌های هم‌مرکز
X, _ = make_circles(n_samples=500, factor=.5, noise=.03, random_state=4)

# اعمال الگوریتم DBSCAN بر روی مجموعه داده
dbscan = DBSCAN(eps=0.1, min_samples=5)
clusters = dbscan.fit_predict(X)

# رسم نمودار
plt.scatter(X[:, 0], X[:, 1], c=clusters, cmap='viridis', marker='o')
plt.title("خوشه‌بندی DBSCAN برای دایره‌های هم‌مرکز")
plt.xlabel("ویژگی ۰")
plt.ylabel("ویژگی ۱")
plt.show()

و به نتیجه زیر خواهیم رسید:

پیچیدگی زمانی DBSCAN

1. حالت بهترین:
   در بهترین حالت، اگر از ساختارهای ایندکس مانند درخت KD یا R-tree برای ذخیره‌سازی و جستجوی نقاط استفاده شود، جستجوی همسایگی هر نقطه در زمان لگاریتمی انجام می‌شود. بنابراین، پیچیدگی کلی الگوریتم به O(nlogn) کاهش می‌یابد. این حالت برای مجموعه داده‌هایی با توزیع مناسب و زمانی که ساختار ایندکس به درستی پیکربندی شده باشد، محقق می‌شود.
2. حالت بدترین:
   در بدترین حالت، اگر از هیچ ساختار ایندکسی برای جستجوی همسایگی استفاده نشود یا تمام نقاط در فاصله ε از یکدیگر قرار داشته باشند، هر جستجوی همسایگی به زمان خطی نیاز دارد. با توجه به اینکه این عملیات برای تمام نقاط انجام می‌شود، پیچیدگی زمانی به O(n²) افزایش می‌یابد. این حالت معمولاً برای داده‌های متراکم یا بدون استفاده از ساختارهای بهینه رخ می‌دهد.
3. حالت متوسط:
   در حالت متوسط، پیچیدگی زمانی به نوع داده‌ها، توزیع آن‌ها و نحوه پیاده‌سازی الگوریتم بستگی دارد. اگر داده‌ها پراکندگی متوسطی داشته باشند و از ساختارهای ایندکس به طور مؤثر استفاده شود، پیچیدگی نزدیک به حالت بهترین خواهد بود. در غیر این صورت، ممکن است به حالت بدترین نزدیک شود.

مزایای الگوریتم DBSCAN:

1. نیازی به دانستن تعداد مراکز خوشه (Centroids) از پیش نیست، برخلاف الگوریتم K-Means.
2. قابلیت شناسایی خوشه‌هایی با هر شکلی را دارد.
3. می‌تواند خوشه‌هایی را که به گروه یا خوشه‌های دیگر متصل نیستند، پیدا کند و با خوشه‌های پر سروصدا نیز به‌خوبی کار می‌کند.
4. نسبت به داده‌های پرت (Outliers) مقاوم است.

معایب الگوریتم DBSCAN:

1. در کار با داده‌هایی که تراکم متغیری دارند، عملکرد مناسبی ندارد.
2. امکان استفاده از پردازش موازی را ندارد، زیرا نمی‌توان داده‌ها را به بخش‌های جدا تقسیم کرد.
3. نمی‌تواند خوشه مناسب را در صورت پراکندگی داده‌ها (Sparse Dataset) پیدا کند.
4. به پارامترهای epsilon و minPoints حساس است.

کاربردهای الگوریتم DBSCAN:

تحلیل داده‌های مکانی:
DBSCAN به دلیل توانایی خود در شناسایی خوشه‌هایی با اشکال دلخواه، برای خوشه‌بندی داده‌های مکانی بسیار مناسب است. این ویژگی در کاربردهایی مانند شناسایی مناطق با استفاده مشابه زمین در تصاویر ماهواره‌ای یا گروه‌بندی مکان‌ها با فعالیت‌های مشابه در سیستم‌های اطلاعات جغرافیایی (GIS) مورد استفاده قرار می‌گیرد.

تشخیص ناهنجاری:
توانایی این الگوریتم در تمایز بین نویز یا داده‌های پرت و خوشه‌های اصلی، آن را برای وظایف تشخیص ناهنجاری مفید می‌سازد. به عنوان مثال، از DBSCAN می‌توان برای شناسایی فعالیت‌های مشکوک در تراکنش‌های بانکی یا تشخیص الگوهای غیرعادی در ترافیک شبکه استفاده کرد.

تقسیم‌بندی مشتریان:
در بازاریابی و تحلیل کسب‌وکار، DBSCAN می‌تواند برای تقسیم‌بندی مشتریان مورد استفاده قرار گیرد. این الگوریتم به شناسایی خوشه‌هایی از مشتریان با رفتارهای خرید یا ترجیحات مشابه کمک می‌کند.

مطالعات محیط زیستی:
DBSCAN در پایش محیط زیست نیز کاربرد دارد؛ برای مثال، می‌توان از آن برای خوشه‌بندی مناطق بر اساس سطح آلودگی یا شناسایی مناطقی با ویژگی‌های محیط زیستی مشابه استفاده کرد.

تحلیل ترافیک:
در مطالعات ترافیک و حمل‌ونقل، DBSCAN برای شناسایی نقاط پر ازدحام ترافیکی یا خوشه‌بندی مسیرها با الگوهای ترافیکی مشابه بسیار مفید است.

نتیجه‌گیری

الگوریتم‌های خوشه‌بندی مبتنی بر چگالی، مانند DBSCAN، با قابلیت شناسایی خوشه‌هایی با اشکال و اندازه‌های متنوع به یکی از ابزارهای قدرتمند در تحلیل داده تبدیل شده‌اند. این الگوریتم بدون نیاز به تعریف تعداد خوشه‌ها، می‌تواند نواحی متراکم را به خوبی تشخیص دهد و داده‌های پرت یا نویز را به عنوان نقاط خارج از خوشه شناسایی کند. این ویژگی‌ها DBSCAN را برای کاربردهایی که داده‌ها دارای ساختار پیچیده و غیرخطی هستند، بسیار مناسب می‌سازد. علاوه بر این، توانایی شناسایی خوشه‌های متراکم در میان داده‌های پراکنده باعث می‌شود که این الگوریتم برای مسائل واقعی با داده‌های غیرمنظم و چندبعدی کاربرد گسترده‌ای داشته باشد.

با این حال، چالش اصلی در استفاده از DBSCAN، تنظیم دقیق پارامترهای ε و minPts است. این پارامترها به دلیل ارتباط مستقیم با توزیع داده‌ها، نیازمند آزمایش و بررسی دقیق هستند و انتخاب نادرست آن‌ها ممکن است منجر به نتایج نادرست شود. به رغم این چالش‌ها، انعطاف‌پذیری DBSCAN در شناسایی خوشه‌ها و کنار گذاشتن داده‌های نویزی، آن را به انتخابی ایده‌آل برای بسیاری از مسائل خوشه‌بندی پیچیده تبدیل کرده است. این الگوریتم، به خصوص در حوزه‌هایی مانند پردازش تصاویر، تحلیل داده‌های جغرافیایی و داده‌کاوی کاربردهای گسترده‌ای دارد.